Quantum Random Numbers in Yao.jl

The first example I use for understanding quantum computing concepts is the Quantum Random Number Generator. It’s also the simplest example possible. Let’s see what it looks like Yao.jl.

As you might expect, it’s beyond trivial.

using Yao, BitBasis
n=3
zero_state(n) |> repeat(n, H) |> measure! |> bint

Here Yao is the base package. BitBasis contains the tools for dealing with bit strings which Yao returns.

We pass a zero_state with n qubits, i.e. $\vert 0^n \rangle$, through n hadamard gates and then measure the result. Each bit has a 50/50 chance of being 0 or 1. In this case we use the bint function from the BitBasis package to convert the measured bits to a number.

The result is indeed a random number between 0 and 7.

Let’s go a little further and make sure the numbers are uniform by plotting the distribution of the results:

results = zero_state(n) |> repeat(n, H) |> r -> measure(r, nshots=10_000) .|> bint

The only difference here is the nshots parameter passed to the measure function to repeat the measurement that many times. This is much faster and cleaner than using a comprehension of something. the .|> operator converts the individual results.

The result is an array of 10,000 measurements which should be uniformly distributed. Let’s check:

histogram(results, legend=:none, xticks=(0:maximum(results)), bar_width=0.9)

Gives us

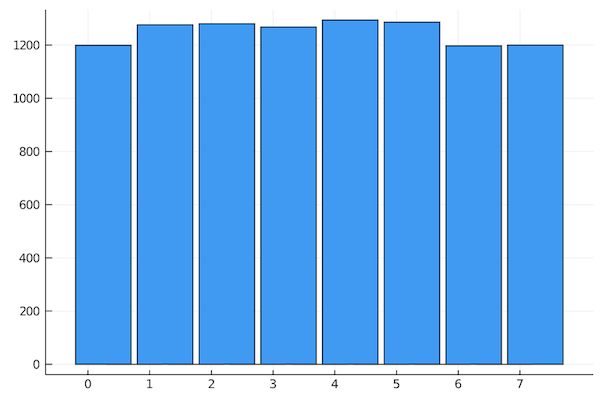
Which is good.