Quantum Random Number Generator

One thing to understand is that, as things stand, quantum computers are not particularly useful. The limited number of quantum bits we have to work with is so limited that classical computers, with over half a century of exponential improvements behind them, beat quantum algorithms at every task.

So why are we interested? Well, we anticipate a point where quantum algorithms will surpass their classical counterparts at some tasks. This is true, for example, with the factoring of semi-prime numbers. That point is known as quantum supremacy and could be years away. What’s more interesting today is that quantum computers represent a new hardware paradigm. There are things that cannot be done way a classical way that can be done using the magic of superposition and entanglement.

The most basic example is the generation of true random numbers which can be implemented trivially on a quantum computer where the probabilistic nature of quantum measurement is the source of randomness. We do this by preparing qubits such that they have a 50-50 change of being true or false when measured, that is in a state lying on the equator of the Bloch sphere.

This can done with a Hadamard gate or a \(\sqrt{NOT}\) gate, that is, the gate that when applied twice would create a \(NOT\) gate. This is simple circuit to generate a random 3-bit number.

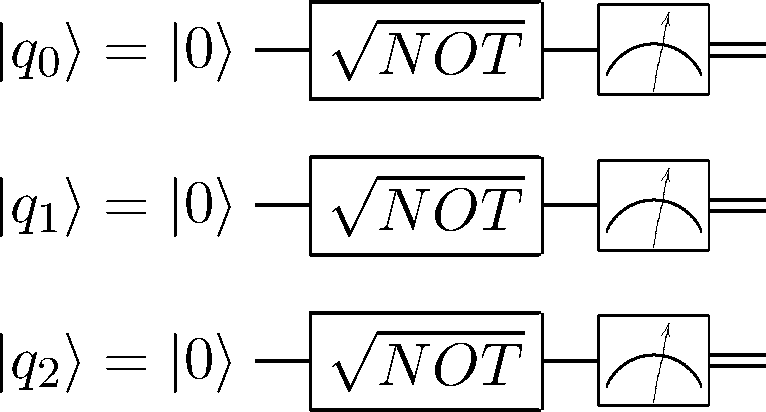
Measurement of \(q_0\), \(q_1\), \(q_2\) will provide 3 random classical binary digits which can be treated as a number between 0 and 7.

In the quko simulator we can write this as:

import java.util.*
import quam.*

val qubits = Qubits(3)
        .halfNot(0)
        .halfNot(1)
        .halfNot(2)
val result = qubits.measureAll()
print(result)             // [false, true, true]
print(result.toInt())     // 3

The result will be a (simulated) random number. Run this algorithm on a real QPU and the number will be truly random.

One thing to notice is that quko interprets the number from top to bottom, MSB first. That is, the result is the binary number \(q_2\)\(q_1\)\(q_0\). This not important here but will be important in other algorithms where the actual value of the result is of interest.