Why Lognormal?

The log-normal distribution is sometimes used as a simple model for the distribution of latencies from real-world systems. ⊕It’s important to understand that models are just models. Under different situations the latency distributions may be completely different. By no means is it a perfect model and sometimes alternatives are better, especially when the load is far below maximum capacity but at high load I’ve empirically found it to be a reasonable fit.

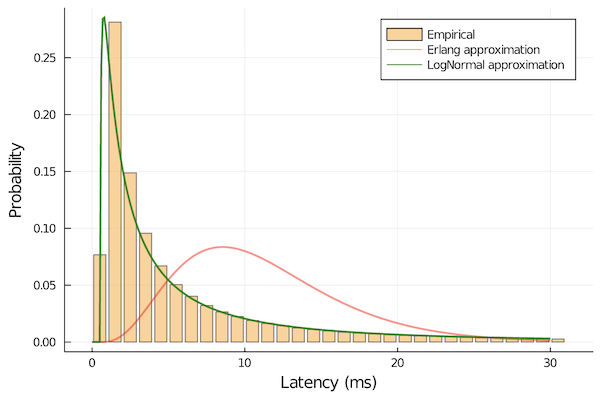
One reason that this is important is that the log-normal is long-tailed. This means that while the average response time under these conditions might be excellent, the top percentiles might be totally unacceptable so we end up having to oversize more than we might like.

I’ve often wondered why this might be the case and answers to this question are often very hand-wavey. Here I attempt a totally unscientific explanation.

Let’s take a standard result from queueing theory and say that the latency is a function of the load factor,$f$, defined as the ratio of arrival rate to service rate.

Latencies fly off to infinity when the load factor approaches 1. Makes sense because if the requests arrive faster than they can be serviced then the queue will grow until something else gives.

Now we might assume there is some dispersal in the load factor due to the natural burstiness of incoming traffic. We don’t want to model this noise with a normal distribution because our load factor is strictly between 0 and 1. A better choice is the beta distribution which has exactly that property and just so happens to nicely approximate the normal distribution if we choose the right parameters.

Now what happens to the distribution of latencies? Well, luck would have it that the transformation of the beta distribution by the formula above gives us the so called beta-prime distribution. And that approximates a LogNormal distribution surprisingly well, especially around the tail.

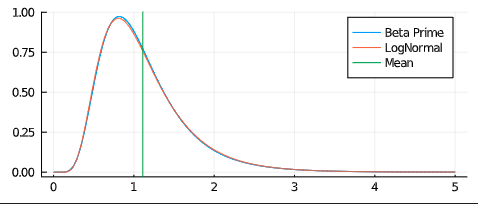
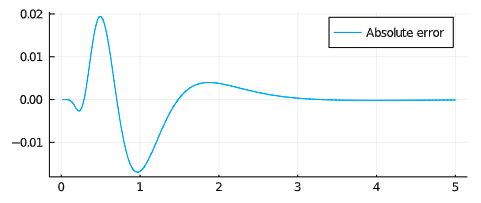
What does this mean? Absolutely nothing and it’s wrong for all kinds of reasons. Nonetheless it might give a clue to the usefulness of the LogNormal distribution and its tail and why the Erlang/Gamma distributions sometimes are more indicative.

The intuition would be that the natural variance in the load produces latencies heavily skewed by the elbow curve of the latency formula, especially when under high load, producing the long tail. Under lower loads the skewing effect is less and the distribution loses it’s long tail, in fact becoming more like an Erlang distribution after all.

Source code for the graphs is here.