Grover's Algorithm in Yao.jl

Continuing the series of posts building the basic quantum algorithms with Yao.jl we come to Grover’s algorithm. There is a tutorial on Grover in the Yao.jl documentation ⊕QisKit also has a nice explication. It’s worth getting multiple perspectives on these things. but I found it a little hard to follow the code so I simplified it right down to the basics.

Remember that we have a binary function, $f$, which is always equal $0$ except for a single value $u$, when it is equal to $1$. The challenge is to find $u$ with as few queries to $f$ as possible. As always, and with all the usual caveats, we take for granted that we have access to an oracle, $U_f$, that provides a suitable quantum transformation based on $f$.

The oracle consists of a transformation which reflects the target value, $u$, and only this value, around the x-axis. All other values are left untouched.

function oracle(u::T) where T<:Unsigned
    n = ceil(Int, log(2, u)) # Use only as many bits as necessary
    v = ones(ComplexF64, 1<<n)
    v[u+1] *= -1 # Flip the value we're looking for
    Diagonal(v)
end

We work out the smallest number of bits needed from the value itself. In the Yao.jl tutorial this is all on one line and quite cryptic, hopefully this version is easier to read.

In the tutorial they use the phased version of the diffusion operator ⊕This diagram is generated directly from the code with YaoDraw :) :

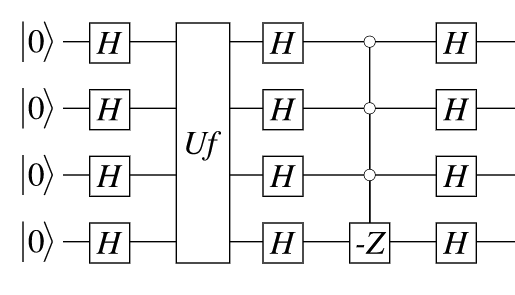
Notice that with this construction we don’t have to use an ancillary bit. As can be seen in the diagram we also have some reusable blocks, namely the $H^{\otimes n}$, which for some reason the tutorial calls gen, and the repeating section which is a combination of the oracle itself followed by the diffusion operator. They are chained together like this:

    gen = repeat(n, H)
    reflect0 = control(n, -collect(1:n-1), n=>-Z) # I-2|0><0|
    repeating_circuit = chain(Uf, gen, reflect0, gen)

Inside the repeating section there is also the reflection circuit, reflect0 which is responsible for flipping the distribution about the average value which is what has the effect of amplifying values made negative by the oracle. To check that it is indeed the correct circuit it can be compared to the other form \(I_n - 2\vert 0^n \rangle \langle 0^n \vert\).

ZERO(n) = foldl(kron, fill([1, 0], n))
Int.(real.(sparse(I, 16, 16) - 2*ZERO(4)*ZERO(4)'))

It is indeed the same, although I’m still sure of the origin of the conditional Z transform version, it’s an identity to bear in mind.

Continuing with the algorithm, the repeating section is simply placed in a for loop applied to a prepared quantum register:

    reg = zero_state(n) |> gen
    for i = 1:iter
        reg |> repeating_circuit
    end

The variable iter is the number of iterations we want to apply. Getting the right value for this is tricky ⊕The tutorial has much more sophisticated way of doing this. so we just use a hand picked value for now. It should be less than $\sqrt{2^n}$. For clarity we wrap the whole circuit in a function and pass in the oracle:

function grovers(Uf::AbstractBlock{n}, iter::Int) where n
...
end
grovers(matblock(oracle(0b11110011)), 10) |> measure!

And that’s it, not too bad actually. Working code is here.

Looking forward to applying to more interesting problems to it.

PS: Just for fun this is how the histogram of probabilities evolves between each iteration. It’s clear how the chosen value emerges in just a few steps.

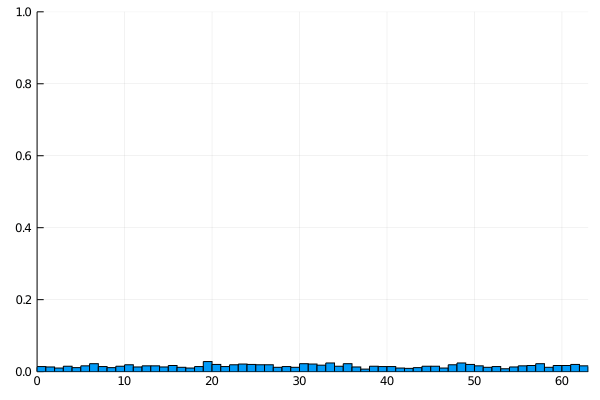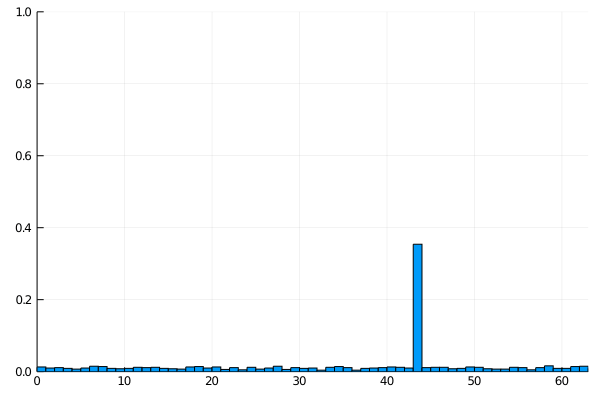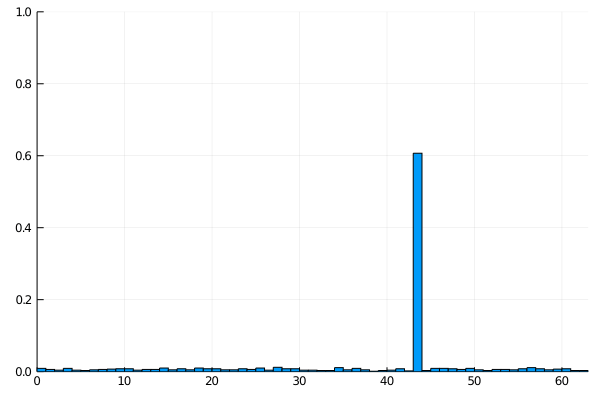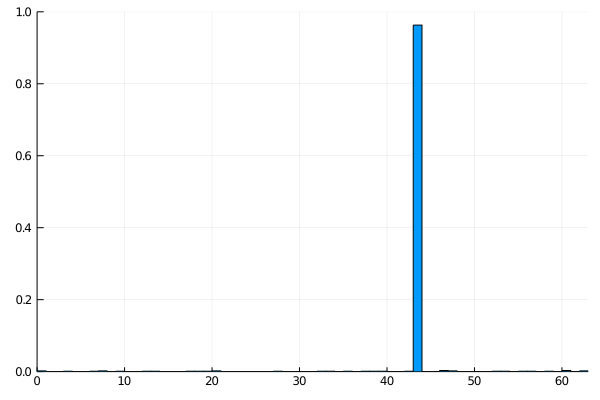
If you’re interested, this is the code to generate the histogram. Run with 6 bits over 6 iterations and 1000 shots at each iteration to get the probability.

using Plots
...
  anim = @animate for i = 1:iter
    numbers = reg |> r -> measure(r, nshots=1000) .|> bint
    histogram(numbers, normed=true, legend=:none, xlims=(0,63), ylims=(0,1), nbins=64)
    reg |> repeating_circuit
  end
...
gif(anim, "grovers-search.gif", fps = 1)