The Deutsch-Jozsa Algorithm

This was one of the first quantum algorithms to be discovered that gave a theoretically significant improvement over the classical equivalent. Having said that it’s not useful at all, its main value was that it served as inspiration for other more practical algorithms such as Grover’s search and Shor’s factoring.

Simplest case

The simplest statement of the problem is to determine if a boolean function, \(f\), always results in the same constant value or if it is balanced and returns both true and false depending on the input.

In programming terms this means evaluating the function:

f : (Boolean) -> Boolean

for both possible inputs and checking the results.

val result = f(false) xor f(true)

In the classical world this will obviously require two evaluations of the function however in the quantum version only one evaluation is ever required.

Imagine we are given a gate \(U_f\) which is based on the function we are interested in. This gate can be constructed in various ways but we’ll assume that it’s given.

Then a circuit for the algorithm can be represented by the following diagram:

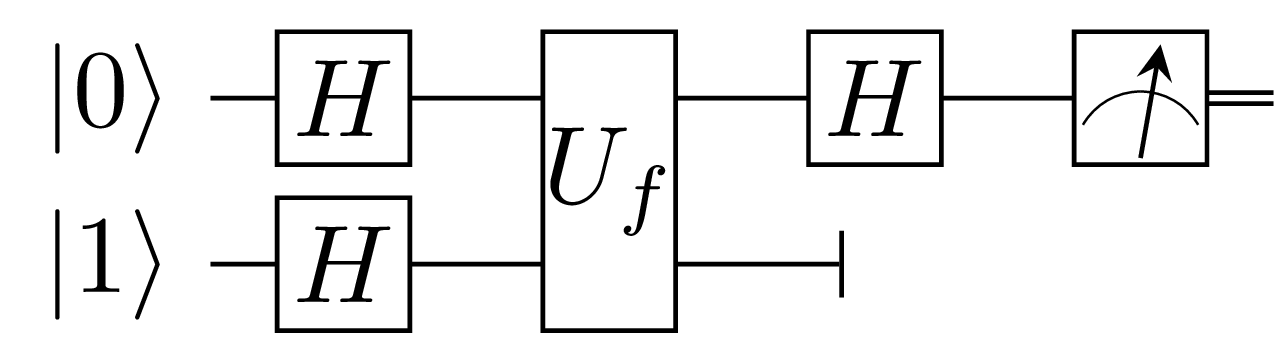
This equates in quko to the following snippet:

Qubits(2)
    .not(1)
    .hadamard(0)
    .hadamard(1)

    .apply(0, 1, oracle)

    .hadamard(0)
    .measure(0)

If the function is balanced then the measurement will always be true, if constant then the measurement will always be false.

One way to think about how this works is that the \(U_f\) gate transforms the superposition of both possible input values. The resulting interference patter provides us with the information we require.

Extending to multiple bits

Other researchers extended to algorithm to multiple bits which corresponds to the function taking an integer argument.

The function becomes:

f : (Int) -> Int

and will, on average, need many more evaluations of the function to test be able to determine if it is constant or not.

The quantum circuit in this case becomes:

We can build this circuit in quko as follows:

private fun isBalanced(n: Int, f: (Int) -> Int) 
    = Qubits(n + 1)
            .not(n)
            .hadamard(0..n)

            .apply(0, oracle(n, 1) { x, y -> f(x) xor y })

            .hadamard(0 until n)
            .measureFirst(n)
            .toInt() != 0

This will give us a boolean result for the given function, assuming the function works on \(n\) bit integers. Note: oracle is a utility function of quko for building the appropriate gate \(U_f\) from the function \(f\).